轻量级的用于开放或闭合麦阵列中的声源定位与追踪方法
要死记硬背的拎出来没事就看看。
优化的轻量级的用于开放或闭合麦阵列中的声源定位与追踪方法
摘要
自然环境中的人机交互需要对环境中的不同的声源进行过滤。这种功能通常需要使用麦阵列,实时的对声源进行定位、追踪,并对不同声源进行分解。同时收集多个麦克风信号并处理分析可以提高对噪音的健壮性,但是麦克风数目的增加也会增加更多的计算量,这限制了响应时间,也限制了机器人的应用场景。声源定位算法会扫描广阔的三维空间以确定声源方位,这需要较多的算力,因此,减少声源定位算法的计算量将能够有效帮助声源定位机器人的场景推广及实施应用。不过,机器人的外形也会限制麦阵列的几何形状。此外,声源定位方法通常会返回一些环境噪音,而这些噪音应该通过声源追踪进行平滑和过滤。本文提出了一种名为SRP-PHAT-HSDA的新的声源定位方法,该方法将结合使用低分辨率和高分辨率的网格以节省扫描空间时对内存的访问。文章将使用一种麦克风指向性模型以减少方位扫描的数目,并忽略掉不重要的麦克风。本文还将引入一种新的麦阵列配置方法,用以自动调整那些平常需要参考麦阵列形状通过经验调试的参数。本文提出了一种对三维卡尔曼方法的改进(简写为M3K),用于生源追踪,该方法可以在三维空间中同时追踪多个声源。本文通过使用包含16个麦克风的阵列和低功耗硬件进行测试,结果显示SRP-PHAT-HSDA和M3K方法仅使用传统算法的1/30到1/4的算力,却能够达到不低于传统声源定位、追踪方法的效果。
关键词:声源定位,声源追踪,麦阵列,实时计算,嵌入式系统,移动机器人,机器人听觉。
1 引言
当发言者离(一个或多个)麦克风较远时进行的语音识别称为远距离语音识别(简称DSR),而远距离会使得背景噪音和反射回响与语音叠加[1, 2],给识别带来困难。不过,DSR可以让发言者在不佩戴手持或头带式麦克风的场景中进行语音识别。尽管,远距离语音识别的健壮性依然是个挑战[3]。麦阵列这种硬件可以在人机交互(简称HRI)中实现DSR。这需要在机器人平台上安装多个麦克风,以处理远距离感知音频,通过过滤机器人平台的风扇、驱动机构,以及环境中不稳定的背景反射声源,在处理速度应当足够快时,实现实时的人机交互交互。这一过程首先需要对感知到的声源进行定位和追踪,然后才能对不同的声源进行分离[4],以进行下一阶段的操作,比如对分离出来的特定语音进行识别[5, 6]。在实现声源定位及追踪方法时,对环境噪音的健壮性以及对计算量的控制十分关键[7],因为这仅仅是实现基于语音的人机交互(HRI)的第一步。在自然环境下实现基于语音的人机交互需要让机器人避免环境中的各种噪音干扰,从嘈杂的背景音中分辨出并识别语音指令。
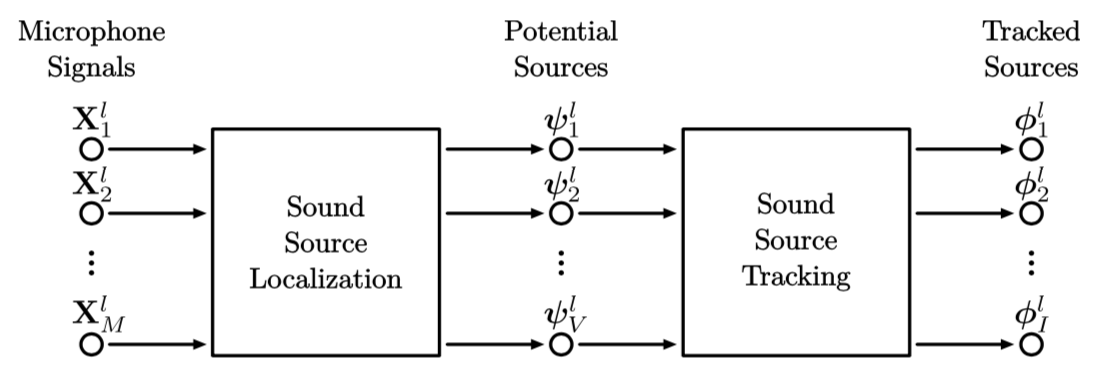
如图1所示,声源定位(简称SSL)以及声源追踪(简称SST)是按顺序依次进行计算的。对于每一帧$l$,SSL使用来自包括$M$个麦克风的麦阵列的音频数据$\mathbf{X}^l=\left{\mathbf{X}^l_1, \mathbf{X}^l_2, \ldots, \mathbf{X}^l_M\right}$生成$V$个潜在声源$\mathbf{\Psi}^l=\left{\psi^l_1, \psi^l_2, \ldots, \psi^l_V\right}$,其中的每个潜在声源$\psi^l_V$由一组表示波达方向(DoA)的笛卡尔坐标$\lambda^l_v$和一个表示可控波束能级组成的$\Lambda^l_v$组成。SSL方法给出由零星的声源(比如稀疏的语音)引起的带噪声源的波达方向,并且同一时间可能存在多个竞争声源。接着,SST利用潜在声源给出$I$个过滤掉噪音的被追踪声源$\mathbf{\Phi}^l=\left{\phi^l_1, \phi^l_2, \ldots, \phi^l_I\right}$,以提供声源的平滑轨迹。改进的SSL和SST方法的功能与所使用的麦克风数量直接相关,而麦克风数量会影响到计算量。
在这一过程中,SSL是最消耗算力的操作,现有不少算法可用于声源定位。Rascon等人[9]提供了一种轻量级的对内存和CPU消耗较低的SSL方法,但是仅支持3个麦克风,而且只能在一个2维平面内进行波达方向计算。Nesta与Omologo[10]提供了一种使用通用状态相干变换实现的声源定位,这一定位方法在多声源场景中尤为有效,但是这一方法中涉及独立成分分析运算(ICA),需要较长时间才能收敛。Drude等人[11]使用基于相位和电平差异的核函数方法,但是这一方法会增加计算量。Loesch和Yang[12]提供了一直基于时域-频域稀疏的定位方法,但这一方法对高混响水平较为敏感。基于标准特征值分解的多信号分类(SEVD-MUSIC)使SSL对加性噪声具有较好的鲁棒性[13]。SEVD-MUSIC最初用于窄带信号[14],不过目前已经可以适用于宽带声源,例如语音[15],并且只要噪音没有被定位信号(如语言)强,这一方法就可以对噪声具有较强的健壮性。基于广义特征值分解(GEVD-MUSIC)方法[16]的多信号分类也用于处理该问题,但这一种方法增加了计算量。基于广义奇异值分解(GSVD-MUSIC)的多信号分类降低了GEVD-MUSIC的计算量,同时提高了定位精度[17],但这一方法仍涉及矩阵特征分解运算。其他方法利用麦阵列的几何特性(线性,圆形或球形)来提高鲁棒性并降低计算量[18,19,20]。尽管这些几何形状产生了有趣的特性,但由于其特定的几何形状也带来了一些物理约束,这些麦阵列配置对于移动机器人的体积限制来说并不太实用。还可以使用具有相位变换的转向响应功率(SRP-PHAT)来实现声源定位。SRP-PHAT通常使用来自成对麦克风的带有相位变换的加权广义互相关(GCC-PHAT)来计算[4,8]。SRP-PHAT比基于MUSIC的方法的计算量更少,但在通过大量麦克风数据扫描3D空间时仍需要大量的计算。随机区域收缩[21]、层次搜索[22,23,24]和矢量化[25]也被研究用SRP-PHAT加速扫描,但通常局限于2维平面和单个资源搜索。Marti[26]等人还提出一种同时在粗网格和细网格上进行递归搜索的方法。这一方法将空间划分为矩形小块,然后将细网格中的多点映射在粗网格的一个点中。不过,这一方法也忽略了麦克风的方向性,并在GCC值上使用了平均窗口,这可能在临近值为负时削减一个峰值的效果。
我们可以把声源追踪方法分为以下四类:
维特比搜索:Anguera等人[27]提出了一种后处理Viterbi方法来追踪时序中的声源。在实时处理数据时,这一方法将引入显著的延迟,因此仅适用于非实时分析。这一方法实现的追踪仅限于离散状态空间,因此该方法仅适用于固定网格中的声源追踪。
顺序蒙特卡罗(SMC)滤波:SMC方法,也称为粒子滤波,能够对单个声源执行低延迟追踪[28,29,30]。 Valin等人[4,8]采用SMC方法来跟踪多个声源。这一方法通过用有限粒子对空间进行采样,以模拟出非高斯的状态分布。SMC可以用来追踪连续空间轨迹,不过这一方法需要大量计算,而且因为使用了随机生成的粒子而不够确定。
卡尔曼滤波:Rascon等人[9]提出了一种基于卡尔曼滤波器的轻量级方法,该方法能够追踪连续轨迹,同时显著减少计算量。然而,该方法仅限于球面坐标中的波达方向,输出高度和方位角,不过,当方位角分辨率随高度变化时,会产生畸变,即引入了方位角隐藏现象。Marković等人[31]提出了一个在李群上的扩展卡尔曼滤波器(LG-EKF),用8麦克风阵列进行方向追踪。LG-EKF解决了方位角隐藏现象,但仅限在2维圆环上进行追踪,因此并不适合追踪3维球面上的声源。
联合概率数据关联过滤(JPDA):Marković等[32]提出了一种可用于3维球面声源追踪的,基于von Mises-Fisher分布上的贝叶斯估计。然而,该方法需要事先知道声源数量,并且忽略各跟踪源的运动模型,这导致当两个声源交叉时会被当做轨迹的切换或融合。
为了改进声源定位和声源追踪,本文提出了一种称为SRP-PHAT-HSDA的SRP-PHAT方法,即按层级搜索指向性模型并自动校准,以及一种使用笛卡尔坐标的改进的3D卡尔曼滤波(M3K)的追踪方法。SRP-PHAT-HSDA首先在粗分辨率网格上扫描3D空间,然后优化特定区域的搜索。该方法利用到达时间差(TDOA)的不确定性模型,通过开放和闭合麦阵列配置,使用多种分辨率水平的网格来优化扫描精度。此方法还使用了麦克风指向性模型,以减少扫描方向的数量,并忽略不重要的麦克风对。M3K用卡尔曼滤波器取代了Valin等人[8]使用的SMC滤波器,并引入了三个新概念:1) 归一化状态以将空间限制为单位球体;2) 推导出计算相干声源的解析解表达式,以加速计算;3) 用于同时跟踪多个声源的卡尔曼均值向量和协方差矩阵的加权更新。这些改进形成了高效的对多个声源的跟踪方法,使之能够嵌入低算力硬件。改进的方法不仅比SMC更节省算力,还解决了卡尔曼滤波在球面座标中的畸变和隐藏。
文章的结构如下:首先,第2节描述了SRP-PHAT与SEVD-MUSIC的计算要求对比,以证明和确定SRP-PHAT-HSDA带来的改进。然后,第3节和第4节分别对SRP-PHAT-HSDA方法和M3K方法进行描述。第5节介绍了在移动机器人上实现8和16圆形麦阵列以及闭合立方麦阵列的实验设置,在3代树莓派上实现了SSL和SST方法。第6节给出了将SRP-PHAT与SRP-PHAT-HSDA方法,以及M3K与SMC方法的对比的实验结果。最后,第7节对文章进行总结,并说明未来工作。
2 SRP-PHAT与SEVD-MUSIC的算力需求
声源定位通常被分为两个子任务:1) 达到时间差估计;2) 在麦阵列周围的3维空间中搜索波达方向。而SRP-PHAT与SEVD-MUSIC方法的主要区别就在于子任务1:SRP-PHAT基于带有相位变换的加权广义互相关(GCC-PHAT)方法,而SEVD-MUSIC基于奇异特征值分解。

